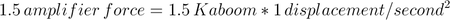
by Danny Maland
Yet another appearance of the disclaimer: Everything that I set before you should be read with the idea that “this is how I've come to understand it.” If somebody catches something that's flat-out wrong, or if you just think that an idea is debatable, please take the time to start a discussion via the comments.
For those who have been following this series from the start, quite a bit of the presented material is “popular” for the analytically-minded audio person. The reason for this is because a lot of the math and science translates directly into usable numbers. Decibels and watts, for instance, are near-instantly usable quantifications of sonic events, or the signals corresponding to sonic events.
By my (admittedly limited) observations, what is far less popular in the mathematical and scientific arsenal of pro-audio folks is classical mechanics. I believe that this is largely, though not exclusively, due to how the numerical output of the relevant equations is not directly useful for pro-audio types. I myself cannot claim to have any desire to know exactly how fast a subwoofer driver accelerates, nor can I claim to have any use for knowing the number of Newtons required to accelerate that driver at a certain rate. However, understanding how aspects of classical mechanics, especially Newton's second law, relate to audio devices can be quite eye-opening.
So – what is this “Newtons” and “Newton's” business? Well, Sir Isaac Newton was the sort of chap who was interested in how and why things moved like they did. He was interested enough to be a developer of the methods of calculus, which is the branch of mathematics that specifically deals with things that are in motion. He also came up with three “laws” of motion, the second of the laws being very important for audio. When you do the kind of work that Newton did, you are very likely to have a scientific unit named after you, and so we got the Newton unit. One Newton is the force required to accelerate a one kilogram object at one meter per second, per second.
For pro-audio folk, Newton's second law is the most immediately important, even if they don't realize it. The second law states that an object accelerates in proportion to the force applied to it, and acceleration is inversely proportional to the object's mass. Put less elegantly, the harder you push on something, the faster it gets moving – and heavy things have to be pushed harder to get them moving at the same rate as light things.
The way this concept boils down is usually presented as “Force equals Mass times Acceleration”:
- As it turns out, this relationship is very important in the audio world – actually, it's critical. The reason for it being critical is because it deals with the make-or-break components that form the entry and exit points of our signal chains. These components are the transducers.
- Transducers are devices which convert one form of energy into a different, yet corresponding form of energy. Microphones, for instance, convert sound pressure waves into electrical signals. Loudspeakers convert electrical signals into sound pressure waves. These two activities, done poorly, can completely negate otherwise excellent devices sitting in between them.
- Since the last few articles have been talking about loudspeakers, let's use a couple of those as an object example. A fictional company, Sonny's Subwoofers makes all kinds of low-frequency loudspeaker drivers. Their basic model is the 15” diameter “Kaboom,” which has a deluxe version in the 18” diameter “Kaboom+.” The Kaboom+ has a diaphragm mass that's 1.5 times greater than that of the Kaboom. Not only is it bigger, but it has more additives to increase its performance – there's more material in it.
- If we invent our own units, we get Figure 2 and Figure 3.
To move the significantly heavier cone of the Kaboom+ at the same rate of acceleration as the lighter Kaboom, the amplifier needs to have the necessary power to let us achieve 1.5 times the physical force on the driver.
There's something else to consider. Newton's first law says that an object in motion will stay in motion unless a force acts upon it. What this means is that that Kaboom+ is not only more difficult to start, it's also more difficult to stop. If the Kaboom+ is not appropriately damped mechanically (designed so that it stops moving as quickly as possible when signal is removed), and the amplifier has trouble damping the driver's movement electrically, the Kaboom+ will have more problems with “ringing” than the basic Kaboom. This ringing causes the sounds produced by the loudspeaker to “smear,” that is, to last longer than they should, and can also cause the loudspeaker to produce entirely unwanted tones.
Important: The above is not to imply that a larger diameter driver is necessarily inferior to a smaller diameter driver. Bad designs come in all sizes. A well-built driver can have a large mass and sound excellent in its intended application. Indeed, we need sufficiently-sized drivers to reproduce low frequency material. Good luck with getting a 1” diameter driver to produce 50 Hz at 120 dB SPLC Slow!
So, what about microphones? If we have two microphones picking up the same airborne sonic event, then (all else being equal), a pickup with low mass will be more sensitive than a pickup with higher mass. Microphone elements with lower mass are inherently superior in terms of their transient response (their ability to react to large changes in level over short time periods), as they have greater acceleration for a given input force. However, better transient response does not necessarily make a microphone better for every application. It is easier to make a rugged microphone if you allow the diaphragm to have a greater mass, and damping that mass to keep it from ringing may not be so difficult as to be prohibitive. It's true that the most accurate microphones available are low-mass devices, but a higher-mass and lower accuracy device may be a better choice for a particular use.
